
1.8 Determining Limits Using the Squeeze Theorem
8 min read•february 15, 2024
Welcome back to AP Calculus with Fiveable! This topic focuses on determining the limit of a function based on information given about other functions that bound it. We’ve worked through determining limits through algebraic manipulation, graphs, and tables, so let's keep building our limit skills. 🙌
⌛ Squeeze Theorem
Before we get into the nitty gritty, be sure to review some of the content we’ve already went over!
📚 Background Knowledge
To effectively use the Squeeze Theorem, you should be familiar with:
- Limits: Understanding how functions behave near a specific value.
- Basic Function Behavior: Knowledge about how functions like sine, cosine, exponential, etc., behave for different inputs.
🧩 What is the Squeeze Theorem?
The squeeze theorem states that if and , then must also . Take a look at the visual below!
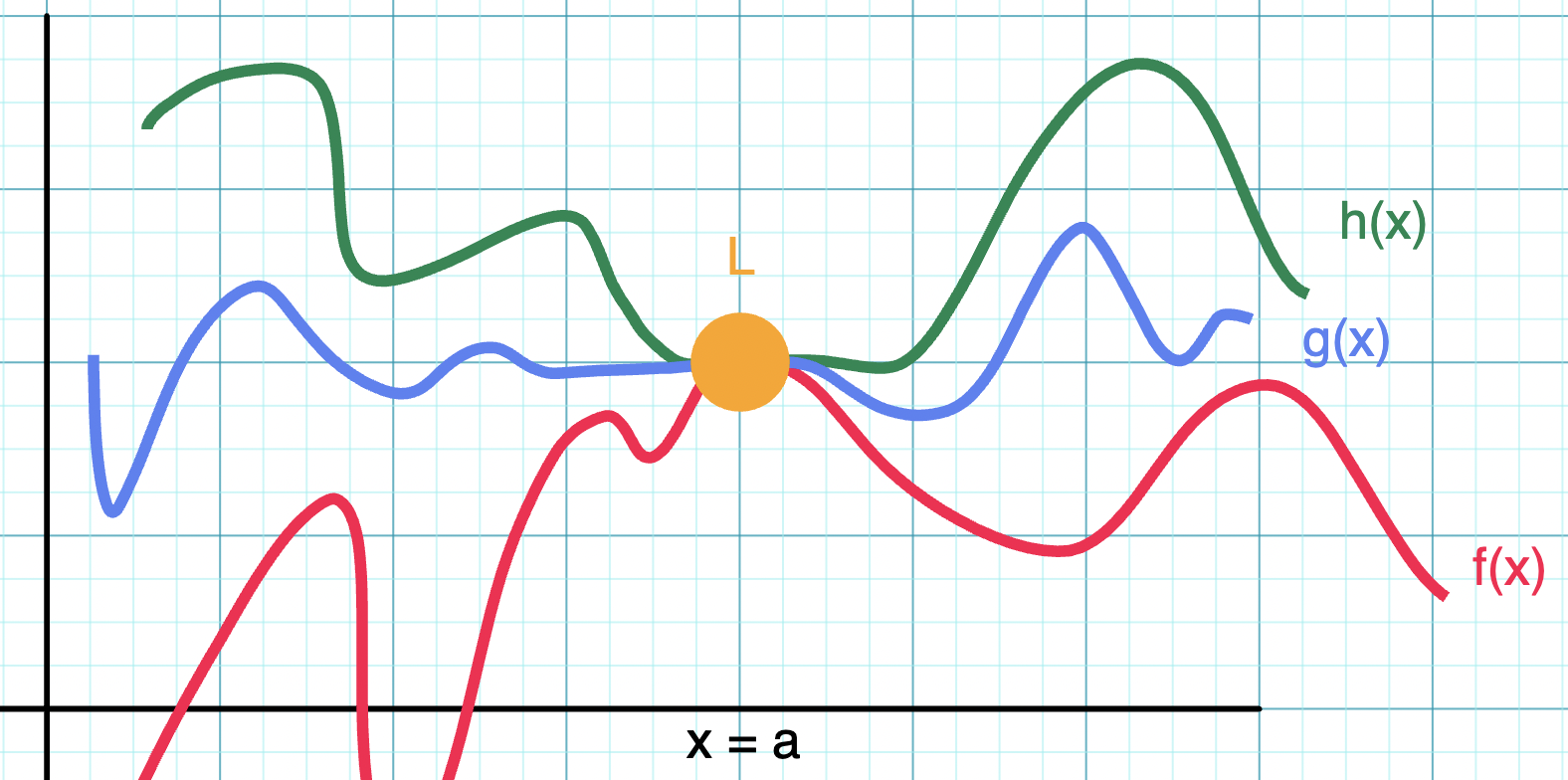
Graph drawn using Virtual Graph Paper
We can see that the function is sandwiched between and , so it must follow the same rule in the shown interval.
🧮 Squeeze Theorem Practice Problems
Let’s work on a few questions and make sure we have the concept down!
1) Squeeze Theorem Logic
Functions and are twice-differentiable functions with It is known that for . Let k be a function satisfying for
. Is continuous at ? Justify your answer.
Once you’re ready, keep on reading to see how to approach this question. ⬇️
If functions and are twice-differentiable, they must be continuous. Therefore, and . Since and the conditions for continuity are met, the squeeze theorem for applies at . So, .
Since , must equal .
We can then conclude that is continuous at because . Brush up on continuity rules with this guide here: Confirming Continuity Over an Interval.
This question is from the 2019 AP Calculus AB examination administered by College Board. All credit to College Board. Way to go! 👏
2) Computing a Limit Using Squeeze Theorem
Find the limit of the function as approaches 0, using the Squeeze Theorem.
In this case, we can use the fact that for all to create a bounding function.
Multiply the inequality by , and then consider the bounding functions and so that .
Since , and the functions are known to be continuous, the Squeeze Theorem can be applied. Let’s check the limits of the bounding functions as they approach 0 to see if they squeeze at .
Because , the Squeeze Theorem holds true, and…
Check out the graph below to confirm our answer visually!
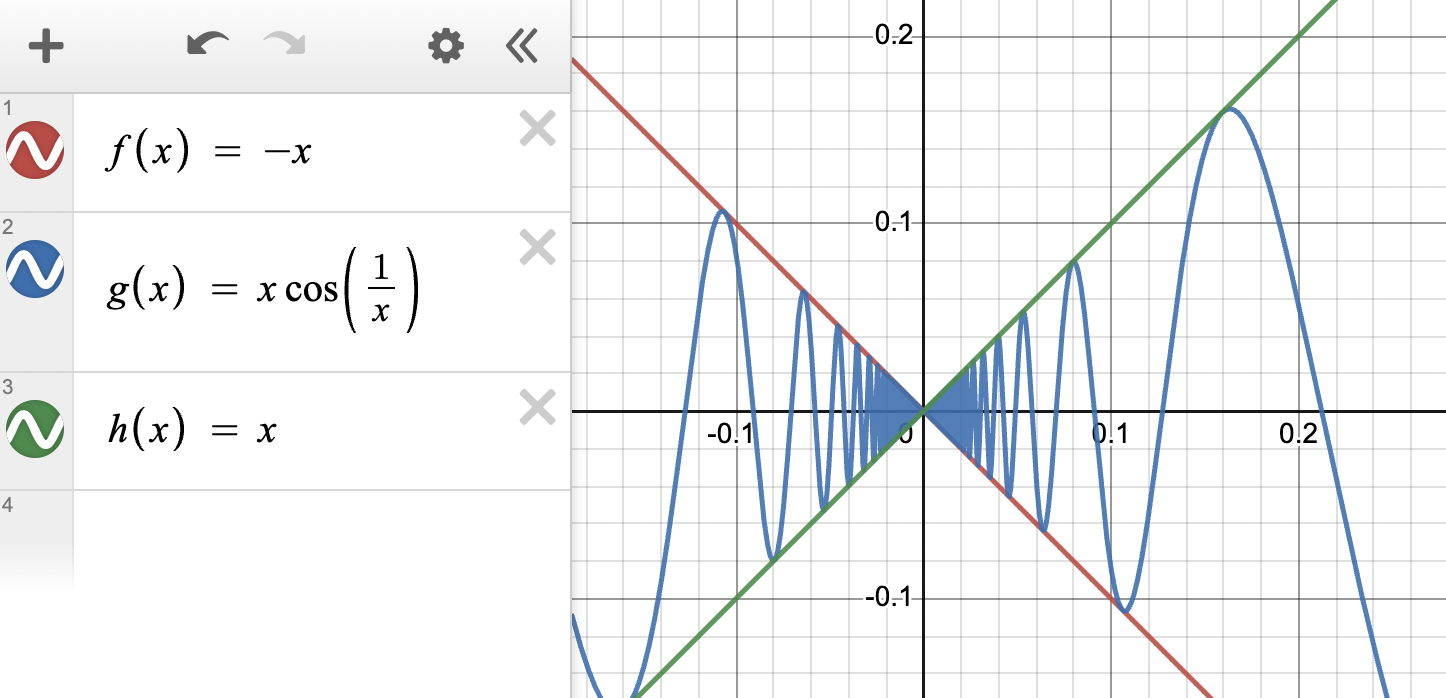
Graph created with Desmos
You nailed it! This was a tough one. 💪
🌟 Closing
Great work! 🙌 The squeeze theorem is a key foundational idea for AP Calculus. You can anticipate encountering questions involving limits and the squeeze theorem on the exam, both in multiple-choice and as part of a free response.

Image Courtesy of Giphy
If you’d like some steps to follow, here they are:
- 🤔 Identifying the Function: Recognize the function for which you need to determine the limit.
- 👀 Finding the 'Squeeze' Functions: Locate two functions that 'squeeze' the given function between them.
- 🏁 Ensuring Known Limits: Confirm that the limits of the 'squeezing' functions are known as x approaches the same value.
You got this! 🤩
Key Terms to Review (6)
Approaches
: In calculus, "approaches" refers to the behavior of a function as the input values get closer and closer to a certain value or infinity. It describes how the output values of the function get arbitrarily close to a specific number or approach a particular limit.Bounded
: A function is bounded if its values are limited or restricted within a certain range. It means that the function does not go to infinity or negative infinity.Function
: A relationship between two sets where each input (domain) value corresponds to exactly one output (range) value.Limit
: The limit of a function is the value that the function approaches as the input approaches a certain value or infinity. It represents the behavior of the function near a specific point.Oscillate
: In calculus, "oscillate" refers to the behavior of a function when it repeatedly alternates between two values without approaching any particular number. It describes functions that exhibit periodic fluctuations around one or more equilibrium points.Squeeze Theorem
: The Squeeze Theorem states that if two functions, g(x) and h(x), both approach the same limit L as x approaches a certain value c, and another function f(x) is always between g(x) and h(x) near c (except possibly at c itself), then f(x) also approaches L as x approaches c.1.8 Determining Limits Using the Squeeze Theorem
8 min read•february 15, 2024
Welcome back to AP Calculus with Fiveable! This topic focuses on determining the limit of a function based on information given about other functions that bound it. We’ve worked through determining limits through algebraic manipulation, graphs, and tables, so let's keep building our limit skills. 🙌
⌛ Squeeze Theorem
Before we get into the nitty gritty, be sure to review some of the content we’ve already went over!
📚 Background Knowledge
To effectively use the Squeeze Theorem, you should be familiar with:
- Limits: Understanding how functions behave near a specific value.
- Basic Function Behavior: Knowledge about how functions like sine, cosine, exponential, etc., behave for different inputs.
🧩 What is the Squeeze Theorem?
The squeeze theorem states that if and , then must also . Take a look at the visual below!

Graph drawn using Virtual Graph Paper
We can see that the function is sandwiched between and , so it must follow the same rule in the shown interval.
🧮 Squeeze Theorem Practice Problems
Let’s work on a few questions and make sure we have the concept down!
1) Squeeze Theorem Logic
Functions and are twice-differentiable functions with It is known that for . Let k be a function satisfying for
. Is continuous at ? Justify your answer.
Once you’re ready, keep on reading to see how to approach this question. ⬇️
If functions and are twice-differentiable, they must be continuous. Therefore, and . Since and the conditions for continuity are met, the squeeze theorem for applies at . So, .
Since , must equal .
We can then conclude that is continuous at because . Brush up on continuity rules with this guide here: Confirming Continuity Over an Interval.
This question is from the 2019 AP Calculus AB examination administered by College Board. All credit to College Board. Way to go! 👏
2) Computing a Limit Using Squeeze Theorem
Find the limit of the function as approaches 0, using the Squeeze Theorem.
In this case, we can use the fact that for all to create a bounding function.
Multiply the inequality by , and then consider the bounding functions and so that .
Since , and the functions are known to be continuous, the Squeeze Theorem can be applied. Let’s check the limits of the bounding functions as they approach 0 to see if they squeeze at .
Because , the Squeeze Theorem holds true, and…
Check out the graph below to confirm our answer visually!

Graph created with Desmos
You nailed it! This was a tough one. 💪
🌟 Closing
Great work! 🙌 The squeeze theorem is a key foundational idea for AP Calculus. You can anticipate encountering questions involving limits and the squeeze theorem on the exam, both in multiple-choice and as part of a free response.

Image Courtesy of Giphy
If you’d like some steps to follow, here they are:
- 🤔 Identifying the Function: Recognize the function for which you need to determine the limit.
- 👀 Finding the 'Squeeze' Functions: Locate two functions that 'squeeze' the given function between them.
- 🏁 Ensuring Known Limits: Confirm that the limits of the 'squeezing' functions are known as x approaches the same value.
You got this! 🤩
Key Terms to Review (6)
Approaches
: In calculus, "approaches" refers to the behavior of a function as the input values get closer and closer to a certain value or infinity. It describes how the output values of the function get arbitrarily close to a specific number or approach a particular limit.Bounded
: A function is bounded if its values are limited or restricted within a certain range. It means that the function does not go to infinity or negative infinity.Function
: A relationship between two sets where each input (domain) value corresponds to exactly one output (range) value.Limit
: The limit of a function is the value that the function approaches as the input approaches a certain value or infinity. It represents the behavior of the function near a specific point.Oscillate
: In calculus, "oscillate" refers to the behavior of a function when it repeatedly alternates between two values without approaching any particular number. It describes functions that exhibit periodic fluctuations around one or more equilibrium points.Squeeze Theorem
: The Squeeze Theorem states that if two functions, g(x) and h(x), both approach the same limit L as x approaches a certain value c, and another function f(x) is always between g(x) and h(x) near c (except possibly at c itself), then f(x) also approaches L as x approaches c.
Resources
© 2024 Fiveable Inc. All rights reserved.
AP® and SAT® are trademarks registered by the College Board, which is not affiliated with, and does not endorse this website.